B5. Функция y = f(x) определена на промежутке (6, 7). На рисунке изображён график производной этой функции
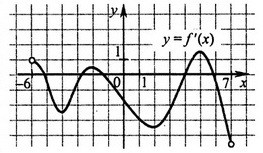К графику функции провели все касательные, параллельные прямой y = 3 + x (или совпадающие с ней).
Найдите количество точек графика функции, в которых проведены эти касательные.У всех прямых, параллельных прямой y = 3 + x, угловой коэффициент равен 1. Угловой коэффициент касательной равен производной функции в точке касания. Поэтому найдём, сколько раз производная принимает значение, равное 1. Для этого найдём число точек пересечения графика производной с прямой y = 1 (параллельной оси OX). Таких точек ровно 2. Ответ: 2 |