Планиметрическая задача. Ромб, подобие, решение прямоугольного треугольника (ЕГЭ-2009, ЕГЭ-2010)
В11. Сторона ромба ABCD равна 4√7, а косинус угла А равен 0,75.
Высота BH пересекает диагональ AC в точке М. Найдите длину отрезка ВМ.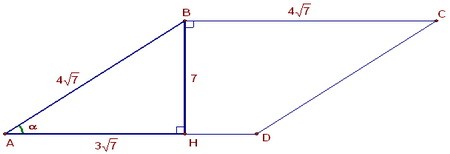

В прямоугольном треугольнике ABH: AH = AB · cosα = 4√7 · 0,75 = 3√7
BH2 = AB2 - AC2 = 112 - 63 = 49; BH = 7.

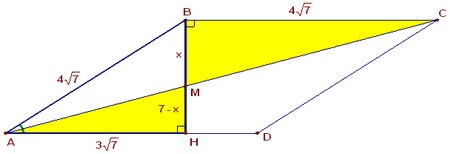Два прямоугольных треугольника ВМС и HMA подобны по двум углам.
Составим пропорцию: BM
HM		 = BC
AH		 = 4
3		.
Пусть BM = x, тогда HM = 7 - x; x
7-x		 = 4
3		; 3x = 28 - 4x; x = 4.
Ответ: 4