С4. Дан прямоугольный параллелепипед ABCDA1B1C1D1. AB = √29, AD = 5, AA1 = 2.
Т. М лежит на отрезке ВС1, т. N лежит на отрезке BD, прямые AM и A1N пересекаются.
Определите тангенс угла между прямой АМ и плоскостью ADD1, если BN : ND = 2 : 3.
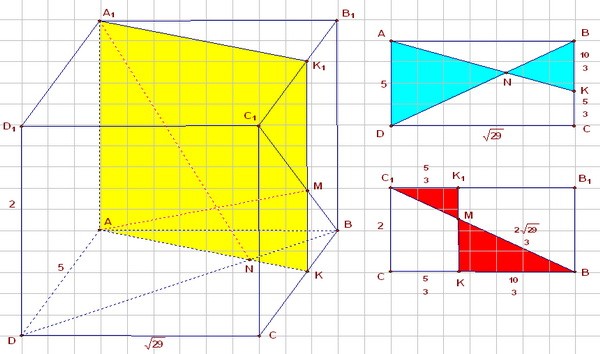 Т.к. прямые AM и A1N пересекаются, то через них можно провести плоскость (жёлтое сечение на рисунке). При этом прямая КК1 окажется параллельной прямой АА1, и точка М лежит на пересечении КК1 и ВС1. На нижнем основании ABCD образуются два подобных треугольника AND и KNB. Учитывая, что BN:ND = 2:3, находим длину отрезка КВ, КВ = 10/3. KC = BC - KB = 5 - 10/3 = 5/3 (см. первый дополнительный рисунок). Рассмотрим боковую грань СС1В1В. Диагональ ВС1 = √4+25 = √29 по теореме Пифагора. Треугольники С1МК1 и ВМК подобны с коэффициентом подобия 0,5. Поэтому МВ = (2/3)·C1B = 2√29/3.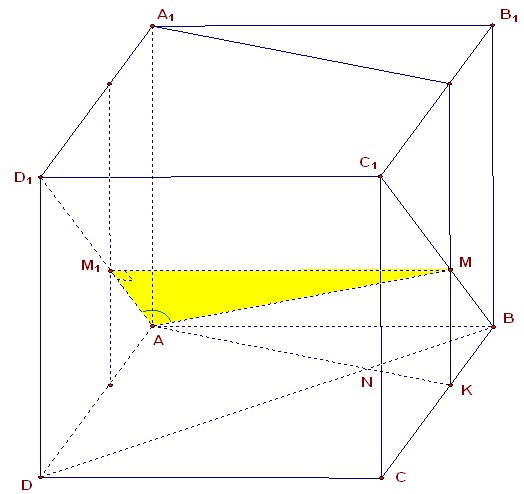 
Углом между прямой АМ и гранью ADD1А1 является угол между прямой и её проекцией на эту грань.
Перпендикуляр из т. М на грань ADD1А1 параллелен и равен АВ, т.е. ММ1 = √29. АМ1 - проекция АМ на ADD1А1.
Рассм. прямоуг. треугольник АМ1М и найдём тангенс угла МАМ1. tgα = MM1 : AM1 = √29 : (2√29/3) = 1,5.
Ответ: 1,5
|