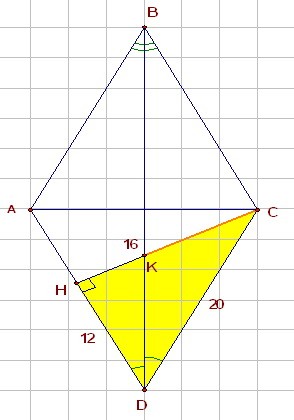
B11. Дан ромб ABCD с острым углом В. Площадь ромба равна 320, а синус угла В равен 0,8.
Высота CH пересекает диагональ BD в точке К. Найдите длину отрезка СК.
 |
1) Так как площадь ромба равна a2·sinB;, где а - сторона ромба,
то из уравнения a2·0,8 = 320 находим сторону ромба а = 20
2) Зная, что sinB = 0,8 и B - острый угол, вычисляем cosB = 0,6.
3) Заметим что в ромбе противоп. углы равны, т.е. угол D равен углу В,
и кроме того, диагональ BD является биссектрисой угла D.
4) Из прямоуг. треуг. CHD находим CH = a·sinD = 20·0,8 = 16,
DH = a·cosD = 0,6a (можно найти и точное значение: DH = 12).
5) В этом же треугольнике применим свойство биссектрисы.
Обозначим СК = х, тогда HK = 16 - x. Составим отношение:
| КСDC | = | КHDH | ; | xa | = | 16 - x0,6a | ; 16 - x = 0,6x; 1,6x = 16; x = 10. |
Ответ: 10
|
|