Параллелограмм, площадь параллелограмма, теорема косинусов (ЕГЭ-2009, ЕГЭ-2010)
B11. В параллелограмме ABCD с площадью 32 диагональ АС равна 2 и угол ACD равен 45° Найти сторону AD.

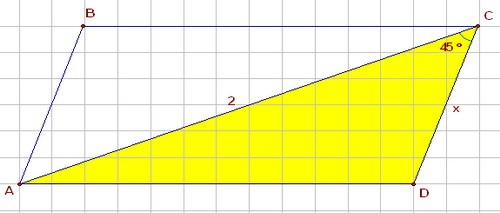1) Т.к. площадь параллелогамма равна 32, а треугольники ABC и CDA равны, то площадь ΔACD равна 16.
2) Найдём площадь ΔACD. S = 1
2		 · CA · CD · sin∠ACD. Получим 1
2		 · 2 · CD · √2
2		 = 16; отсюда CD = 8√2.
3) В этом же ΔACD применим теорему косинусов. AD2 = AC2 + DC2 - 2 · AC · DC · cos∠ACD;
AD2 = 4 + 128 - 2 · 2 · 8√2 ·√2
2		 =132 - 32 = 100; AD = 10.
Ответ: 10