В11. В параллелограмме ABCD биссектриса угла В пересекает сторону СD в точке T и прямую AD в точке М.
Найдите периметр треугольника ABM, если BC = 15, BT = 18, MT = 12.
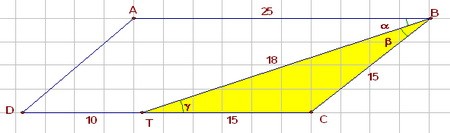1) ∠α = ∠β, так как ВТ - биссектриса угла В по условию задачи.
∠α = ∠γ как внутр. накрест лежащие углы при параллельных прямых АВ и DC и секущей TB.
Следовательно, ∠β = ∠γ, значит, ΔTBC равнобедренный и ТС = ВС = 15. Тогда DT = 25 - 15 = 10.
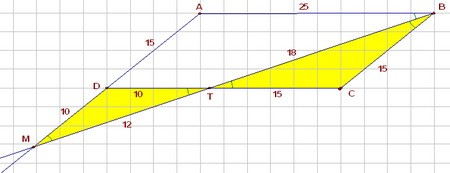2) Треугольники MDT и BCT подобны по двум углам. Значит, ΔMDT тоже равнобедренный и MD = 10.
| Кроме того, из подобия найдём MТ: | МТТВ | = | МDCB | ; | МТ18 | = | 1015 | ; MT = 12. |
3) Наконец, находим периметр треугольника ABM: AB + BM + AM = 25 + (12 + 18) + (10 + 15) = 80.
Ответ: 80
|
