|
С5. Даны два уравнения:
√4(2 - 3p)x + 5(5 + 12p) = 2x + 2p + 1 и
(1 + 61/(p+2))x = 51 - x.
Значение параметра p ≠ -2 выбирается так, что число различных корней
первого уравнения равно сумме числа p+1 и числа различных корней второго уравнения.
Решите второе уравнение при каждом значении параметра, выбранном таким образом. Первое уравнение может иметь один или два разл. корня, а может корней и не иметь, т.к. имеет вид √kx+b = cx+d и при возведении в квадрат становится квадратным. Второе уравнение имеет вид ax = 51-x (где a>1), у него всегда единственный корень,т.к. слева возрастающая показательная функция, проходящая через т.(0,1), а справа - убывающая линейная функция, проходящая через т. (0,51).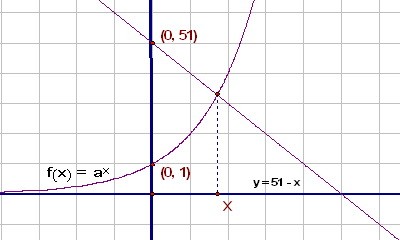 
Если z - число корней первого уравнения, то из условия следует равенство
z = p + 1 + 1, т.е. z = p + 2. Т.к. p ≠ -2, то z ≠ 0, а значит, z = 1 или z = 2.1) Если z = 1, то p = -1. Убедимся, что первое уравнение имеет только один корень. √20x - 35 = 2x - 1; 20x - 35 = 4x2 - 4x + 1; 4x2 - 24x + 36 = 0; x2 - 6x + 9 = 0; x = 3. Подставив х=3 в уравнение, получаем верное равенство. Корень единственный. Теперь решим второе уравнение для p = -1. Получаем 7x = 51 - х, отсюда x = 2. (корень единственный и находится подбором) 2) Если z = 2, то p = 0. Проверим, имеет ли первое уравнение два корня. √8x + 25 = 2x + 1; 8x + 25 = 4x2 + 4x + 1; 4x2 - 4x - 24 = 0; x2 - x - 6 = 0; x = 3, x = -2. Условию 2x + 1 ≥ 0 удовлетворяет только х = 3. Это единственный корень. Таким образом, при p = 0 второе уравнение решать не требуется. Ответ: при p = -1 корень второго уравнения 2 |