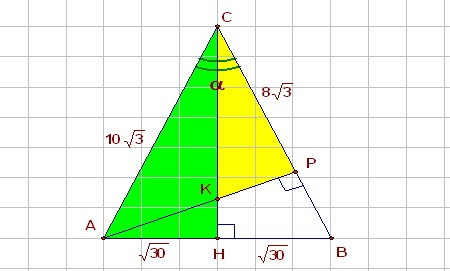
В11. Площадь равнобедренного треугольника ABC равна 90, а боковая сторона равна 10√3.
К основанию АВ и стороне ВС проведены высоты СР и AH, пересекающиеся в точке К.
Найдите площадь треугольника CKH.
1) Из формулы площади треугольника ABC найдём синус угла при вершине: S = 0,5 · AC · BC · sin∠C;
0,5 · 10√3· 10√3 · sin∠C = 90; 150√3 · sin∠C = 90; sin∠C = 90/150 = 9/15 = 3/5; sin∠C = 0,6.
2) По условию отрезки высот пересекаются, значит, треугольник ABC остроугольный, и cos∠C = 0,8.
3) В прямоугольном треугольнике ACP находим катет. СP = AC · cos∠C = 10√3 · 0,8 = 8√3.
4) Прямоугольные треугольники ACH и KCP подобны по двум углам (CH является биссектрисой).
Значит, площади этих треугольников относятся как квадрат коэффициента подобия.
Коэффициент подобия равен отношению отрезков СH и CP. Найдём длину высоты СH.
5) По теореме косинусов в треугольнике ABC найдём основание. АВ2 = AC2 + BC2 - 2 · AC · BC;
АВ2 = 300 + 300 - 2 · 300 · 0,8 = 600 - 600 · 0,8 = 600 · 0,2 = 120; AB = 2√30; AH = AB/2 = √30.
6) Из треугольника ACH по теореме Пифагора: CH2 = AC2 - AH2 = 300 - 30 = 270; CH = 3√30.
| 7) Таким образом, находим коэффициент подобия: k = | CPCH | = | 8√33√30 | = | 83√10 | . |
| 8) Отношение площадей равно квадрату коэффициента, т.е. k2 = | 6490 | = | 3245 | . |
| 9) Учтём, что площадь треуг. ACH равна половине площади треуг. ABC, т.е. 45. |
| 10) Наконец, находим площадь искомого треугольника СKH: S = | 3245 | · 45 = 32. |
Ответ: 32
|
